Supreme Info About What Is The Node Rule In A Circuit

Understanding the Node Rule

1. What's This "Node Rule" Everyone's Talking About?

So, you're diving into the world of circuits? Awesome! You'll quickly hear about something called the "node rule." Don't let the name intimidate you; it's actually quite simple. Think of a node as a meeting point, a junction where multiple wires (and therefore, multiple currents) come together in a circuit. The node rule, also known as Kirchhoff's Current Law (KCL), is all about what happens at these meeting points.

Imagine a water pipe splitting into multiple smaller pipes. The amount of water flowing into the junction must equal the amount of water flowing out of the junction. Otherwise, water would either disappear (impossible!) or pile up at the junction (also impossible in a stable system!). The node rule says the same thing about electrical current: the total current entering a node must equal the total current leaving the node. It's all about conservation—what goes in must come out.

Mathematically, we express this as: I_in = I_out. In plain English, the sum of all currents going IN to a node equals the sum of all currents going OUT of the node. Some people prefer to express it as I = 0, where currents entering are positive, and currents leaving are negative (or vice versa—just be consistent!). This means the algebraic sum of all currents at a node is zero.

Why is this important? Well, it's fundamental to analyzing and understanding how circuits work. It allows you to calculate unknown currents if you know some of the other currents in the circuit. Without this rule, circuit analysis would be a whole lot harder—trust me!

Digging Deeper

2. Mapping the Circuit Landscape

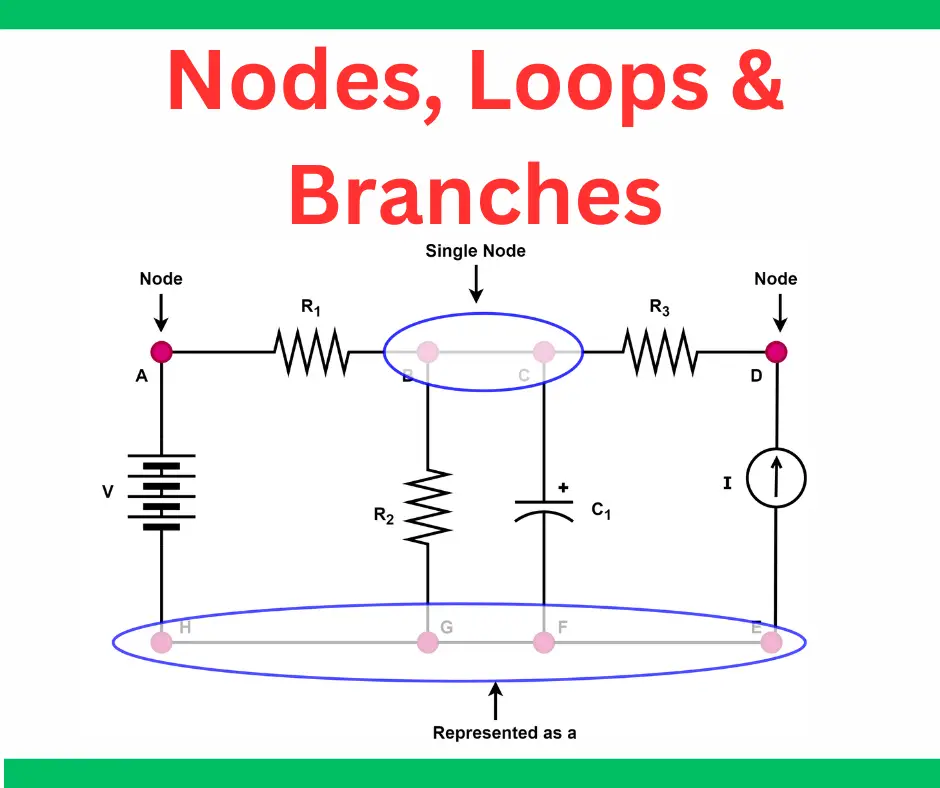
Let's clarify some key terms. A node, as we've already established, is a connection point between two or more circuit elements. A branch is a single path connecting two nodes, and it can contain one or more circuit elements (resistors, voltage sources, current sources, etc.). A loop is any closed path in a circuit that starts and ends at the same node.

Think of a road network. Cities are like nodes, roads are like branches, and a round trip starting and ending in the same city is like a loop. Current flows through branches, and the node rule ensures that the flow balances at each city (node).

So, how do you apply the node rule in practice? First, identify the nodes in your circuit. Then, carefully label the currents flowing into and out of each node. You might not know the values of all the currents, but that's okay—give them variable names (like I₁, I₂, I₃). Finally, apply the node rule equation ( I_in = I_out) to each node. This will give you a set of equations that you can solve to find the unknown currents.

It's crucial to correctly identify the direction of current flow. If you guess wrong, don't worry! The math will sort it out. You'll simply get a negative value for the current, indicating that it's actually flowing in the opposite direction of your initial guess. Just keep your signs consistent within each equation.

Putting the Node Rule to Work

3. Show Me the Money (or, You Know, the Current)

Let's look at a simple example. Imagine a node where three wires connect. Wire 1 has a current of 2 Amperes (A) flowing into the node. Wire 2 has a current of 3 A flowing into the node. Wire 3 has a current, let's call it I₃, flowing out of the node. What is the value of I₃?

Applying the node rule, we have: I_in = I_out. So, 2 A + 3 A = I₃. Therefore, I₃ = 5 A. Simple as that! The current flowing out of the node must be 5 A to balance the current flowing in.

Now, let's make it a little trickier. Suppose we only know that I₁ = 2 A (flowing in) and I₃ = 1 A (flowing out). What is I₂ if we know it is also flowing out? Then we have: 2 = 1 + I₂. This means I₂ = 1 A flowing out.

Remember, the node rule works for any number of branches connected to a node. Just make sure you account for all the currents and their directions. Practice makes perfect, so try working through some circuit examples to solidify your understanding.

Common Mistakes and How to Avoid Them

4. Navigating the Pitfalls of Node Analysis

Applying the node rule seems straightforward, but there are a few common mistakes people make. One is forgetting to account for all the currents at a node. Make sure you've identified every branch connected to the node and assigned a current to it. Another common mistake is getting the current directions wrong. If you're unsure, just guess a direction and let the math tell you if you're wrong (a negative sign will indicate the opposite direction).

A frequent issue arises from inconsistent sign conventions. Decide whether currents entering the node are positive or negative, and stick with that convention throughout the entire analysis. Mixing and matching signs will lead to incorrect results. A helpful tip is to draw arrows clearly indicating the direction of each current, which makes it easier to apply the rule correctly.

Furthermore, always ensure that the units are consistent. If currents are given in milliamperes (mA), convert them to Amperes (A) before applying the node rule, or the results will be incorrect. Double-checking your work and units is always a good practice in circuit analysis.

Finally, remember that the node rule only applies to nodes. Don't try to apply it to a branch or a loop. It's specifically about the balance of currents at a connection point.

Node Rule FAQs

5. Clearing Up the Confusion

Still have some questions swirling around? Let's tackle some common FAQs about the node rule:

Q: What happens if I get a negative current value?

A: A negative current value simply means that the actual current is flowing in the opposite direction of what you initially assumed. Don't panic! Just remember that the magnitude of the current is correct; only the direction is reversed.

Q: Can I use the node rule on any circuit?

A: Yes, the node rule (Kirchhoff's Current Law) applies to any electrical circuit, regardless of its complexity. It's a fundamental law of circuit analysis.

Q: Is the node rule the same as Kirchhoff's Current Law (KCL)?

A: Yes, the node rule is just another name for Kirchhoff's Current Law (KCL). They are the same thing.

Q: Does the node rule apply to AC circuits as well as DC circuits?

A: Yes, the node rule applies to both AC and DC circuits. In AC circuits, you need to consider the phase of the currents, but the principle remains the same: the total current entering a node must equal the total current leaving the node.