One Of The Best Tips About How To Solve KVL And KCl
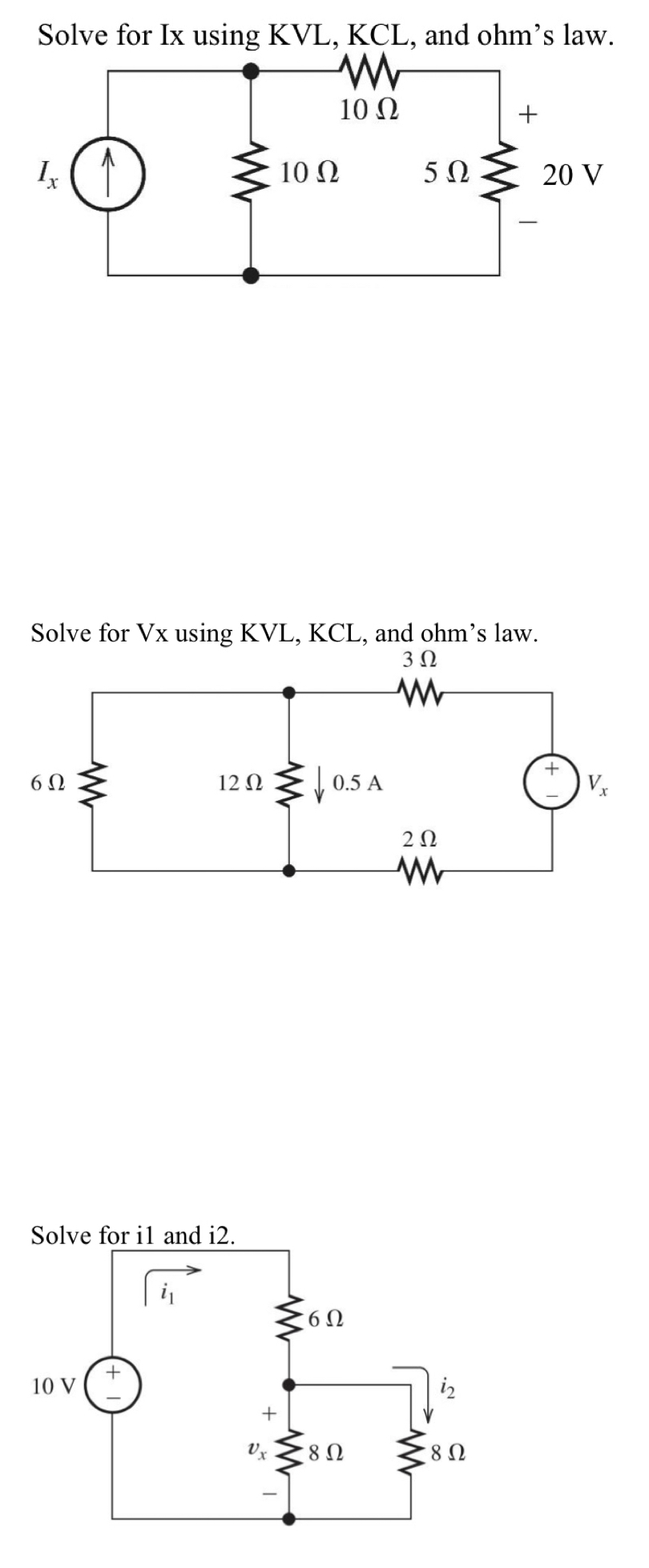
Solved Solve For Ix Using KVL, KCL, And Ohm's Law.
Understanding Kirchhoff's Laws
Ever stared at a circuit diagram and felt your brain short-circuit? Don't worry, you're not alone! Electrical circuits can seem intimidating at first, but with the right tools, you can conquer them. Two of the most important tools in your electrical engineering arsenal are Kirchhoff's Voltage Law (KVL) and Kirchhoff's Current Law (KCl). Think of them as the Sherlock Holmes and Dr. Watson of circuit analysis — solving mysteries one equation at a time.
These laws might sound complicated, but they're based on simple, fundamental principles. Basically, KVL deals with voltage, and KCl deals with current. They ensure that energy and charge are conserved within a circuit, maintaining balance and order. Without them, circuits would be chaotic, unpredictable, and frankly, pretty useless.
This isn't just some dry academic exercise, either. Understanding KVL and KCl is crucial for anyone working with electronics, from hobbyists building robots to engineers designing complex power systems. They're the key to understanding how circuits behave and predicting their performance, which ultimately lets you build better, more efficient gadgets. Get ready to embark on this journey of demystifying electrical circuits. We're diving deep, and it's going to be electrifying!
Consider them the foundation upon which you'll construct your understanding of electrical circuits. Master them, and you'll be well on your way to becoming a circuit-solving guru. Let's get started by explaining each law separately!
1. What is Kirchhoff's Voltage Law (KVL)?
KVL, also known as Kirchhoff's Second Law (though we usually just stick with KVL), states that the sum of all voltage drops and voltage sources around any closed loop in a circuit must equal zero. Think of it like this: if you start at a point in a circuit and travel around a complete loop, the total voltage you gain and lose must balance out. No voltage mysteriously appears or vanishes! Imagine hiking a mountain; what you gain in altitude going up, you lose coming down back to the starting point.
Mathematically, KVL can be expressed as: V = 0, where represents the sum and V represents the voltage. This means that if you add up all the voltages (considering their polarities, of course) around any loop, the result will always be zero. Its like a cosmic balancing act for voltage within a circuit.
Applying KVL involves identifying closed loops within the circuit. A closed loop is any path that starts at a point and returns to the same point without crossing any components twice. Once you've identified a loop, you need to assign polarities to the voltage drops across each component. This is where things can get a little tricky, but with practice, it becomes second nature. Remember that current flows from the positive terminal to the negative terminal of a resistor, creating a voltage drop.
So, how do you actually use KVL? Let's say you have a circuit with a voltage source and a couple of resistors in series. You can apply KVL by starting at the voltage source, going around the loop, and adding up the voltage drops across each component. If you know the values of the resistors and the voltage source, you can then solve for any unknown voltages in the circuit. Its all about setting up the equation and letting algebra do its magic!
2. What is Kirchhoff's Current Law (KCl)?
Now let's tackle KCl, also known as Kirchhoff's First Law. KCl states that the sum of all currents entering a node (a junction point in a circuit) must equal the sum of all currents leaving that node. It's all about conservation of charge. Imagine a pipe splitting into multiple smaller pipes; the total amount of water entering the junction must equal the total amount of water leaving the junction.
Mathematically, KCl can be expressed as: Iin = Iout, where Iin represents the sum of currents entering the node and Iout represents the sum of currents leaving the node. In simpler terms, what goes in must come out. It's a fundamental principle that ensures charge doesn't build up or disappear at any point in the circuit.
Applying KCl involves identifying nodes within the circuit. A node is any point where two or more circuit elements are connected. Once you've identified a node, you need to determine which currents are entering the node and which currents are leaving the node. Assigning directions to the currents is crucial for getting the signs correct in your KCl equation.
So, how do you put KCl into practice? Imagine a node with three branches connected to it. If two currents are flowing into the node, and one current is flowing out of the node, KCl tells us that the sum of the two incoming currents must equal the outgoing current. If you know the values of two of the currents, you can easily solve for the third using KCl. It's a simple yet powerful tool for analyzing current flow in circuits.
3. KVL and KCl in Action
Let's say we have a simple series circuit with a 12V battery and two resistors, R1 (2 ohms) and R2 (4 ohms). We want to find the current flowing through the circuit and the voltage drop across each resistor.
First, we apply KVL around the loop: 12V - V1 - V2 = 0, where V1 is the voltage drop across R1 and V2 is the voltage drop across R2. We know that V = IR (Ohm's Law), so V1 = I 2 ohms and V2 = I 4 ohms. Substituting these into our KVL equation, we get: 12V - I 2 ohms - I 4 ohms = 0. Simplifying, we have 12V = I 6 ohms.
Solving for I, we find that I = 2 amps. Now that we know the current, we can find the voltage drop across each resistor: V1 = 2 amps 2 ohms = 4V, and V2 = 2 amps * 4 ohms = 8V. Notice that 4V + 8V = 12V, which confirms that KVL holds true.
This simple example demonstrates how KVL and Ohm's Law work together to solve for unknown quantities in a circuit. By applying KVL, we were able to relate the voltage drops across the resistors to the source voltage. And by using Ohm's Law, we were able to relate the voltage drops to the current flowing through the resistors. With these two tools, you can tackle a wide range of circuit problems.
4. Tips and Tricks for Mastering KVL and KCl
Assigning Current Directions: Always clearly define the direction of current flow in each branch of the circuit. Consistency is key! If you assume a direction incorrectly, don't worry; your answer will just be negative, indicating the actual direction is opposite to what you assumed. Think of it as the circuit politely correcting your initial guess.
Choosing Loops Wisely: When applying KVL, select loops that minimize the number of unknown variables in your equations. This will make the equations easier to solve. Sometimes, a clever choice of loops can dramatically simplify the problem.
Simplifying Circuits: Before applying KVL and KCl, simplify the circuit as much as possible by combining resistors in series and parallel. This can reduce the number of equations you need to solve and make the analysis more manageable. Its like decluttering your workspace before tackling a big project.
Double-Checking Your Work: After solving for all the unknowns, always double-check your results to ensure that KVL and KCl are satisfied at all nodes and loops. This is a crucial step in catching any errors and ensuring that your solution is correct. Think of it as proofreading your work before submitting it.
5. Beyond the Basics
KVL and KCl aren't just for simple resistor circuits. They're also essential for analyzing more complex circuits containing capacitors, inductors, and transistors. While the specific equations might look different, the fundamental principles remain the same: voltage loops must sum to zero, and current must be conserved at nodes.
For example, when analyzing circuits with capacitors and inductors, you'll need to use differential equations to describe the relationship between voltage and current. However, KVL and KCl still provide the framework for setting up these equations and solving for the circuit's behavior over time.
Similarly, when analyzing circuits with transistors, you'll need to use transistor models to represent the behavior of these devices. However, KVL and KCl are still crucial for analyzing the surrounding circuitry and determining the operating point of the transistor.
In essence, KVL and KCl are the bedrock of circuit analysis, regardless of the complexity of the circuit. They're the tools that every electrical engineer and electronics enthusiast needs to master. So, practice them diligently, and you'll be well on your way to becoming a circuit-solving pro!
[Solved] Circuit Applying KVL, KCL & Ohm's Law Solve For The Voltage V
Frequently Asked Questions (FAQs)
6. Q
A: Absolutely! While we've focused on DC circuits in our examples, KVL and KCl are equally applicable to AC circuits. The only difference is that you'll be dealing with complex numbers (phasors) to represent the sinusoidal voltages and currents. But the fundamental principles remain the same — voltage loops must sum to zero, and current must be conserved at nodes.
7. Q
A: No problem! If you assume the wrong direction for a current, your calculated value will simply be negative. This indicates that the actual current is flowing in the opposite direction to what you initially assumed. Just flip the direction in your diagram and use the positive value for your calculations. Its like a self-correcting mechanism!
8. Q
A: Yes, there are several powerful software tools that can assist you with circuit analysis. SPICE (Simulation Program with Integrated Circuit Emphasis) is a widely used simulator that can solve complex circuits using KVL, KCl, and other circuit analysis techniques. There are also various online circuit simulators that offer user-friendly interfaces and can handle a wide range of circuit types.


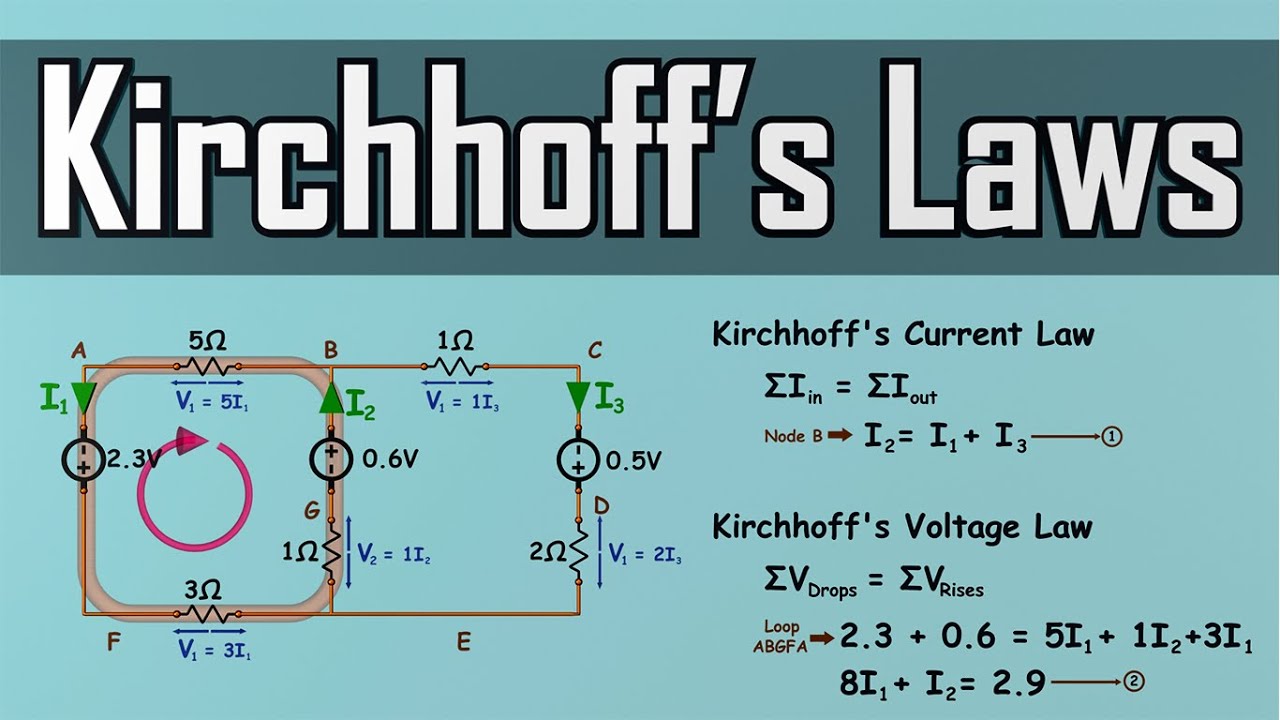
Kirchhoff's Laws How To Solve A KCL & KVL Problem Circuit Analysis
